HELP FILE FOR: DESIGN OF PLATE TYPE LIFTING LUGS:

Updated 07 June 2012

DEFINITION:

Plate lugs are used to lift horizontal equipment such as storage tanks, equipment skids, modules, structures, etc. They are also used to lift vertical equipment that must be upended such as cold boxes, refinery vessels, etc. The lower part of the lug plate is welded to the side of a structure, equipment skid, beam or vessel shell with a three or four sided weld.

The design of a lifting lug is made up of four parts; the lug plate, the weld size used to connect it to a shell or structure, the bearing stress at the pin hole and the end area of the lug. The design of a lifting lug is very critical and must be done to the latest standards and codes.

For design reference, the program assumes that the lug is in the vertical position with the pin hole at the top. Further, the line of the force is assumed to be in the plane of the strong axis and the angle of the force on the lug is measured from a horizontal reference line thru the center of the pin hole. For example, at zero (0) degrees, the force would be at a right angle to the longitudinal centerline of the lug. At ninety (90) degrees, it would coincide with the longitudinal centerline of the lug. See the plate lug drawing below.

The design of the end area and bearing of the lifting lug are based on the total force on the lug applied in the vertical. Their design is also based on the radius of the lug and not on the width of the lug base. The combined stress of the lug plate and the weld size are calculated from the vertical and horizontal components of the force at the specified angle. These stresses are based on the width of the lug base.

PROGRAM OBJECTIVE:

The objective of this program is to provide a design for the end area of a plate type-lifting lug that is efficient and safe. It will also check the bearing stress at the pin hole and the combined stress of the lug plate and the weld. It can also be used to check these same values for an existing lug design. The output information conforms to the requirements of AISC and ASME B30.20.

If the plate lug is being used to upend a piece of equipment, ie, as top head lugs or cone lugs, the lifting force on the lugs increases as the lift angle increases. See example 2 below to see how the program handles a variable force applied to a plate lug.

EXAMPLES OF PLATE LUG USE:

1. Six plate lugs were used to lift the jet fuel storage tank shown in the photo below and were connected using three sided welds. In this case, four sided welds could have been used, as there was access to make a weld on the backside of each lug at the top of the tank, but the extra capacity was not needed as the force on the lugs was at 90 degrees.

2. A 400 ton vertical vessel with two plate lugs. The plate lugs are called top head lugs in this application and are connected to the shell with three sided welds, as it is not possible to make the fourth weld on the backside of the lug at the tangent line.

3. Erecting a vertical vessel with two plate lugs. The plate lugs are called cone lugs in this application and are connected to the shell with three sided welds, as it is not possible to make the fourth weld on the backside of the lug at the tangent line of the cone.

4. Erecting a cold box with four plate lugs. They are connected to the shell with four sided welds, as the top weld on the backside of the lug is accessible in this application.

WHAT THE PROGRAM DOES NOT DO:

The program does not:

1. Check the sum of the pad radius + pad weld + lug weld for a plate lug to see if it is less than the eccentricity. The reasoning is that the program user might want to decrease the combined stress of the lug plate and the lug weld size by decreasing the eccentricity. This could be done by cutting a flat segment off the bottom of the pad next to the lug weld. The pad could be cut off as close as 1” (25 mm) to the bottom edge of the lug hole with out structurally affecting the lug design. The pad weld size would then need to be proportionally increased to account for the lose of weld length. See example 3 below.

2. Check the sum of half the width of the lug plus the sling diameter plus 1’’ (2.54 cm) clearance to see if it is less than the distance from the center of the shackle pin to bearing on the bail.

3. Compare the required lug weld size to the thickness of shell or support.

This comparison should be made to determine if a lug with a larger cross-sectional area should be used or if a reinforcing pad is required under the lug to lower the weld size.

In any case, the weld size should not exceed the lug thickness or the shell/support thickness.

4. Check a plate lug used as a cone lug or top head lug to see if the shackle eye or the lug pads will interfere with the top of the kicker plate. See the top head lug drawing below to see where the kicker plate is located.

5. Analysis the local stresses in the shell or support caused by the force on the lug. The local stresses should be analyzed to see if a reinforcing pad is required under the lug to spread out the load, or if the structure needs to be stiffened to prevent over stressing.

These five checks are left up to the program user.

FOR A FIRST TRY IN THE DESIGN OF A LIFTING LUG:

The dimensions of some Crosby shackles are included in the lookup table in the program. Note, all the Crosby shackles are rated in metric tons. Shackle sizes up to 150 metric ton (Te) are model G 2130, sizes over 150 Te are G 2140. The user can select a shackle size from the table based on the force seen by the lug and the dimensions will be imported into the appropriate fields of the program. The dimensions of a lug that has been designed for that shackle size will also be imported into the appropriate fields of the program. If the lug dimensions are not exactly what are required, the user can then fine-tune the design, i.e., increase and/or reduce the force, change the angle of the force, increase the lug width, change the eccentricity, etc, so that it fits the purpose and still meets code.

The lug designs are based on a force at 60 degrees, Fy = 36 ksi (2.53 Te/cm^2), allowable force on the weld = 14.85 kips/in (1.04 Te/cm) and the I.F. = 1.8

If a shackle size is not listed that the user would like to consider, then the user can click on the SHACKLE button, input the shackle description, for example “Crosby G2130x4.75”, and then input its dimensions and appropriate lug dimensions directly into the fields of the program. The Crosby Group website www.thecrosbygroup.com lists all of their available shackles with dimensions in ENGLISH and METRIC units. For other shackles with dimensions listed in METRIC units, the user will have to refer to other sources.

When the program displays an error message about the lug dimensions, it is sometimes helpful to decrease the force on the lug until the output fields are displayed. This allows the user to see all of the output results and get an idea of which input information to change. As this information is changed, the force on the lug can then be increased to its original value

TOTAL FORCE:

The total force on the lug is input as kips (1 kip = 1,000 lbs.) in the English version and metric tons (Te) in the Metric version.

The Crosby shackles shown in both look up tables are all rated in metric tons, ie the SWL of the Crosby 2130x85 is 85 metric tons. In designing lugs for these shackles, it has been found that in several cases the maximum capacity of the shackle could not be used because the required lug is to wide for the shackle. This is without using a smaller safety factor, using lug material that has a Fy greater than 36 ksi or using a larger angle of the force on the lug, ie 90 degrees. So, to keep things simple, the force on the lugs in the look up tables have been limited to twice the SWL of the shackles as though they were rated in US tons. For example, click on the sample values and note that for a Crosby 2130 x 85 that the force on the lug used is 170 kips for the English version and 77.11 Te for the metric version. The program user is free to design a lug using a force on the lug equal to the SWL of the shackle, which in the above case is 187.39 kips or 85 metric tons. As stated above, to do this, it might be necessary to reduce the impact factor or increase the Fy or use an angle on the lug greater than 60 degrees.

When the program displays error messages about the lug dimensions, it is sometimes helpful to decrease the force on the lug until the output fields are displayed. This allows the user to see all of the output results and get an idea of which input information to change. As this information is changed, the force on the lug can then be increased to its original value.

It is important to remember, that for a constant force but applied at different angles on the lug, the worst case for combined stress for the lug plate and the lug weld is at approximately 20 degrees with the horizontal.

SIDE LOADING OF THE LUG:

When plate lugs are used to upend a vertical vessel, a kicker plate should be added to the side of the lug as shown in the top head lug drawing in example 2. This will reduce the side loading to the lug plate due to the force not acting in the plane of the strong axis. Bending stress of the lug in the weak axis would be calculated at this point and not at the top of the weld group or the top tangent line. The maximum expected side force on the lug should be used to determine the thickness of the kicker plate.

Also, the eccentricity of the lug plate above the top of a tank or skid frame should be kept as small as possible.

IMPACT FACTOR:

A minimum impact factor of 1.80 should be used for new design in order to conform to AISC and ASME B30.20 which limits stresses to .33*Fy. By using 1.80, the allowable stresses can be used as printed in the AISC Manual.

The program allows a variable impact factor to be used so that when checking an existing design, the impact factor can be determined that was used to calculate the stated allowable load for the lifting lug. If the impact factor turns out to be less than 1.8, the program user will then have to make a decision as to the structural integrity of the lug based on its application and the risk involved.

The program limits the impact factor to 1.25 or greater.

ANGLE OF THE FORCE ON THE LUG:

With the lifting lug in the vertical position with the pin hole at the top, the angle of the force is measured from a horizontal reference line running through the center of the pin hole. Therefore, if the force is acting at a right angle to the lug, it is at zero degrees. If the force is acting in the vertical direction along the longitudinal centerline of the lug, it is at 90 degrees.

LUG PIN HOLE DIAMETER:

It is recommended that a lug pin hole diameter be used that is 0.13” (0.33 cm) greater than the shackle pin diameter for shackles up to 150 tons (136 Te) and 0.25” (0.64 cm) for shackles sizes larger than that. If a smaller shackle pin diameter is used than the above recommendation, the bearing stresses will be higher. If a larger shackle pin diameter is used than the above recommendation, the pin might not fit up with the hole in the lug due to manufacturer and fabrication tolerances.

For the first try in the design of a lifting lug, the user can select the appropriate shackle from the lookup table in the program based on the force on the lug. The dimensions of the shackle and a pre-designed lug will automatically be entered into the appropriate input fields in the program.

LUG RADIUS:

After the user enters all of the input values and clicks on calculate, the program will check to make sure that the “lug radius” is equal to or greater than the output value for the “maximum effective lug radius”. If the lug radius is smaller, the program will prompt the user to enter a larger radius.

NOTE:

1. If the program allowed a lug radius to be used that is smaller than the maximum effective lug radius, then the “maximum allowable end area” would be smaller than the area required past the pin hole.

2. “The maximum allowable end area” is calculated using the “maximum effective lug radius”, so using a “lug radius” that is larger than the maximum effective lug radius will not result in an increase in the maximum allowable end area, only an increase in the actual end area.

3. The maximum effective lug radius is a requirement per AISC to prevent the design of the lug beyond the pin hole from being long and thin, ie subject to buckling.

LUG PLATE THICKNESS:

The selection of the thickness of the lug plate should be limited to those sizes available. Installing pads is an additional cost, so generally it is more economical to use a thicker lug plate whenever possible in lieu of using pads.

It is not recommended to weld two lug plates together to get the desired lug plate thickness.

WIDTH OF THE LUG PLATE AT THE BASE:

Plate lug dimensions vary from lug to lug, depending on the designer’s criteria and the application. The most common type of plate lug is where the width of the lug plate equals two times the radius of the lug and the distance from the top of the weld group to the pin hole (the eccentricity) is determined by the radius of the pads, the lug weld size, the pad weld size, the radius of the shackle eyes, an obstruction on the structure, etc.

Some lugs are wider at the base than two times the lug radius, due to the need for additional weld length, more bending strength, etc. The lugs are connected to the side of a skid, structure or vessel shell with a three sided or a four sided weld configuration.

No matter what the shape of the lug is, the design of the end area is based on the lug radius and not on the width of the base. This is why most designs are very conservative concerning the area of the lug across the pin hole and the most important consideration is the area past the pin hole. See sections A-A and B-B on the lug sketch above.

LUG SIDE WELD LENGTH:

It is recommended that the side weld length be approximately equal to 0.7 * width of the lug base. The ratio between the side weld length and the width of the lug base can be smaller or greater than 0.7, but a higher ratio yields a lower required weld size.

ECCENTRICITY:

The eccentricity is the dimension from the top of the weld group to the center of the lug pinhole. This value is used to calculate the bending in the lug plate and the lug weld size due to the horizontal component of the force. The program checks to make sure that the eccentricity is greater than the sum of the shackle eye radius plus the actual lug weld.

NOTE: Increasing the eccentricity to satisfy the above check will increase both the combined stress and lug weld size. Therefore the eccentricity will probably need to be increased in increments of 0.25” to 0.5” (0.64 cm to 1.27 cm).

If the angle of the force on the lug is increased to say 90 degrees, then the lug weld size will decrease and the eccentricity can be decreased accordingly.

Lowering the eccentricity can reduce the combined stress of the lug plate and the lug weld size. This can be done by cutting off the bottom segment of the lug pads. To see how this can be done; go to example 3 in the HELP file for the pad eye lugs. This example applies to plate lugs as well.

LUG PADS:

Pads are usually designed and welded to the lug plate when the actual bearing stress is greater than the allowable bearing stress. Some times they are used to increase both the end area and to reduce the bearing stress.

The pads should be welded to the lug plate and then the pinhole line bored so that even bearing is obtained between the pads and the lug plate. There is a DIN standard that allows the I.D. of the pad holes to be larger than the I.D. of the lughole. Using pads of this design will provide more end area but will do nothing for bearing.

In order to allow sufficient room for the weld between the lug and the pad, it is recommended that for an initial try the user should use a pad radius 0.5 in (1.27 cm) smaller than the lug radius. The program will check to see if the sum of the pad radius plus the pad weld is greater than the lug radius. In looking at the output information, the user can then increase the pad radius if there is more than enough room for the pad weld.

INSIDE WIDTH OF THE SHACKLE:

It is recommended that the sum of the thickness of the lug plate plus the thickness of the pads plus 0.25 in. (0.64 cm) clearance be equal to or smaller than the actual inside width of the shackle measured at the pin. The program will check this clearance. The user can fool the program and decrease the 0.25 in. (0.64 cm) clearance to say 0.15 in. (0.38 cm) by entering the shackle width 0.10 in. (0.25 cm) larger than it actually is.

LUG PAD WELDS:

The weld sizes for the pads in this program are based on using LH 60 rod and a force on the weld of 9.6 kips/in.

THREE SIDED LUG WELDS VS FOUR SIDED LUG WELDS:

Welding vertically down both sides and horizontally across the bottom of a plate lug is called a three-sided weld. This is the most commonly used weld configuration. If access is available to make an additional horizontal weld on the backside of the lug and at the top of the frame/structure, then this weld configuration is called a four-sided weld. Often, a doubler pad is welded to the side of a vertical vessel with a four-sided weld and a lug plate is welded to the doubler pad with a three-sided weld. This is usually done when the shell thickness is less than the required size of the three-sided weld. The thickness of the doubler pad would have to be equal to or greater than the size of the three-sided weld. The dimensions of the doubler pad would have to be large enough so that the weld size required to connect it to the shell of the vessel would be equal to or less than the shell thickness.

The program calculates the weld size required for both a three-sided weld and a four-sided weld configuration. The program user must decide which weld configuration is applicable for his application.

In the top head lug drawing below, note that the shell is 0.38” thick and the required three-sided lug weld size is 0.75”. A 0.75” thick doubler pad is welded to the shell with a four-sided weld size of 0.38”. The eccentricity of 26” is required to provide shackle clearance between the vessel head/insulation. This distance was obtained by making a layout to scale similar to the end view on the lug drawing. This distance must be used to determine the bending stress in the lug plate and the required lug weld size. It is measured from the top of the weld configuration (in this case from the top tangent line) up to the centerline of the lug pinhole. The kicker plate shown on the right side of the drawing is used to stiffen the lug plate extending beyond the tangent line. Bending in the weak axis would then be about this kicker plate and not at the tangent line.

EXAMPLE 1: Using the program with English Units.

The “sample values” button at the bottom of the input screen contains input for a typical plate lug problem where the force on the lug is at a specific angle. By clicking on “sample values” the input values are shown with the output values blank. By then clicking on “calculate”, both the input and output values are shown.

EXAMPLE 2:

UPENDING A VERTICAL VESSEL WITH TWO PLATE LUGS

(The plate lugs are called Top Head lugs in this application)

Plate lugs are welded to the shell of a vertical vessel and are then used to upend the piece of equipment from the horizontal to the vertical as shown in the photos above. In this case, the force on the lugs increases as the lift angle of the equipment increases. The following procedure shows how to calculate the bearing and end area of the lug, the combined stress on the lug plate and the weld for this type of lift. The photo shows two plate type-lifting lugs with three sided welds being used to lift a 170-ton vertical vessel. For this example, the vertical force on each plate lug will be 170 kips at the set position. .

It requires two runs of the plate lug program to determine the required output values. It requires three runs if a doubler plate is required between the plate lug and the shell. In order to simplify data entry, use the sample input values from example 1 where the force on the lug is 170 kips.

For the first run of the plate lug program, change the lift angle from 60 degrees to 90 degrees. Leave the 170 kips as the force on the lug because this value will be the load on the lug with the vessel in the vertical position. Change the width of the lug to 26”, the side weld length to 16” and the eccentricity to 26”. Leave all of the other input values as they are. See the top head lug drawing below for all of the dimensions. This drawing is very similar to the top head lug drawing actually used for the lugs in the photos.

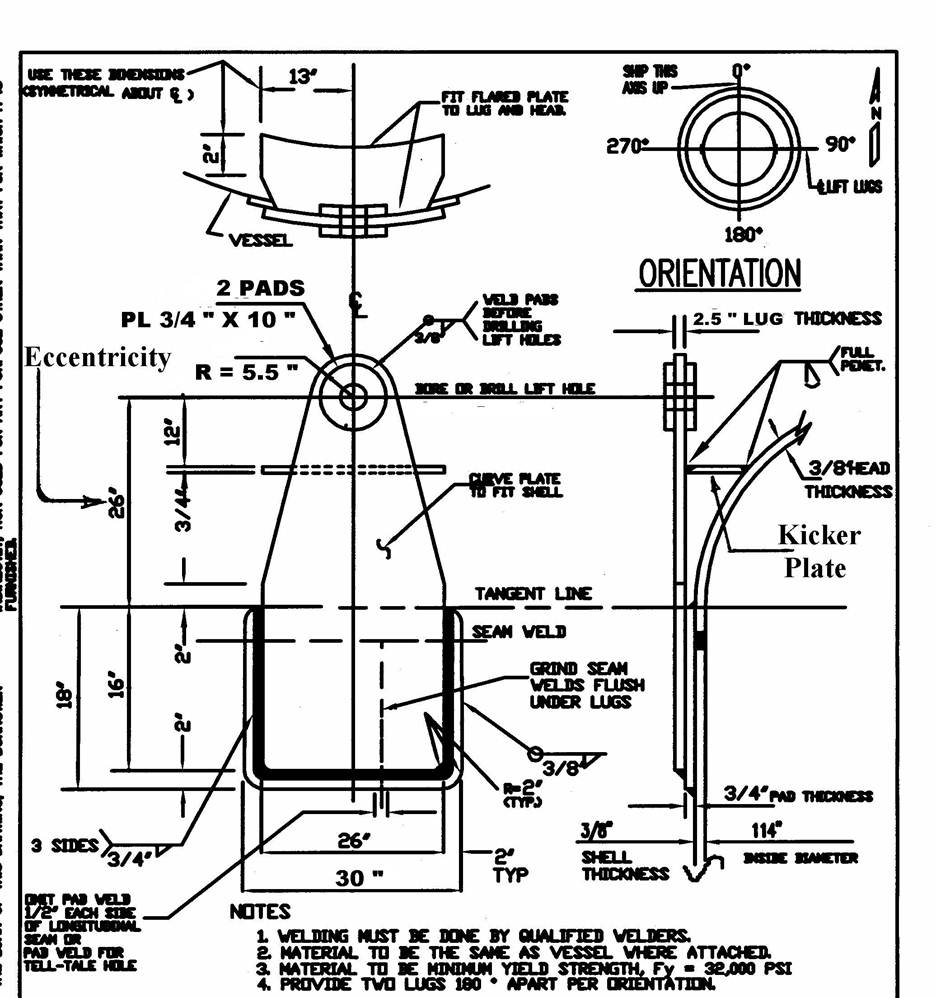
TYPICAL TOP HEAD LUG DRAWING

Calculate and note that the combined stress check on the lug plate is 0.22, the three-sided weld size is 0.36”, and the bearing and the lug calculations are acceptable. Make a printout of this run, but note on it that the values for the combined stress of the lug plate and lug weld size are not applicable and their maximum values will be determined by the second run.

To make the second run of the plate lug program, the side force on the lug needs to be known for the equipment lift angle of 0 degrees, ie, when the vertical vessel is in the horizontal (IPP). The user can calculate this force by hand or go to the upending forces program in the same section of the website as this program, click on the sample values and change the total weight to170 kips, the total length to 120’, the lower length to 48’ and the offset length to 5.5’. Run the program and make a printout the same as the one below.

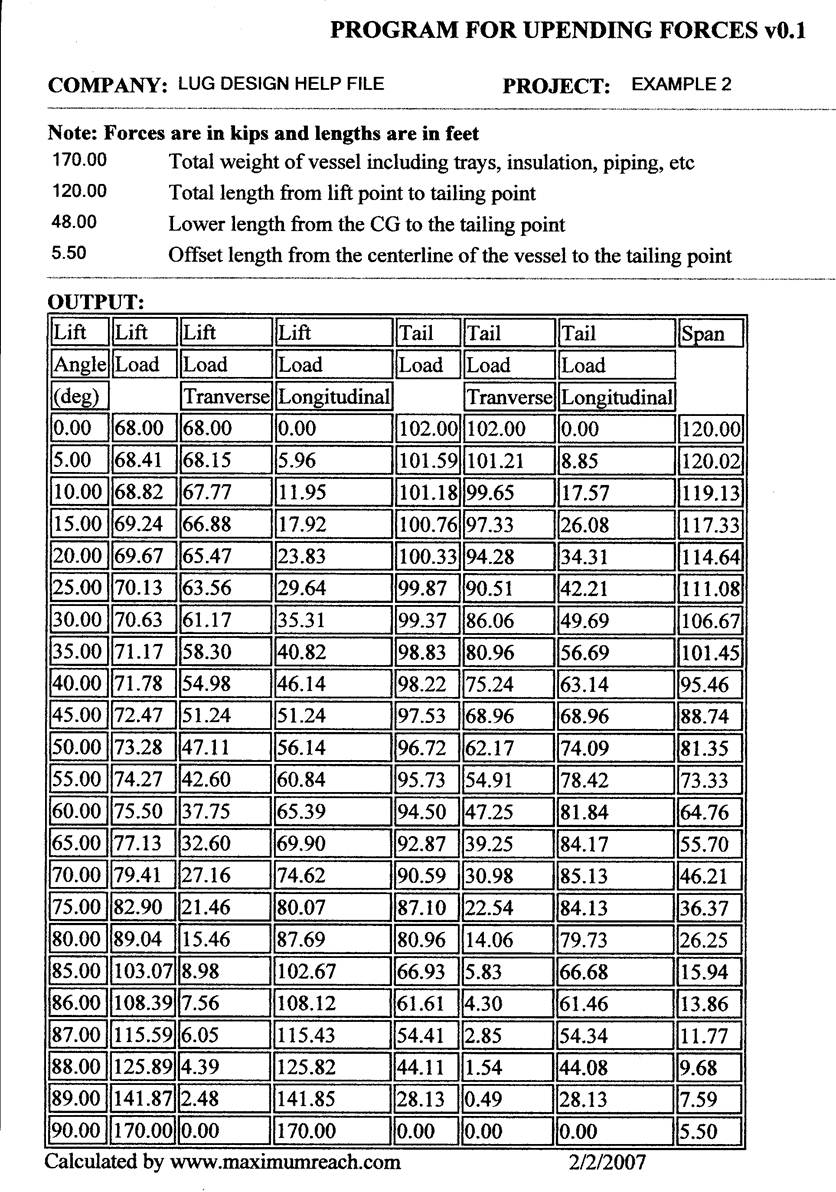
Note that at a 0 degrees lift angle, the transverse force = 68 kips.

Now make the second run of the plate lug program using zero as the lift angle and 68 kips as the force on the lug. Keep all of the other input values the same. Make a printout of this run where the lift angle is 0 degrees and the force on the lug is 68 kips. Use this run as your second plate lug run. Again, mark out the information on the bearing and end area as not being applicable for this lift angle and load.

As the shell thickness of the vertical vessel in this example is only 0.38” thick, then the three sided weld size of 0.74” is to large. To solve this problem, the width of the lug plate could be increased to 30.0”. This is the maximum recommended arc length for this diameter of vessel based on a 30 degree included angle, ie the arc length = 0.01745 * 57”outside radius of vessel * 30 degrees = 30”. The side weld length could be increased to 40.0”. After calculating, this would yield a three-sided lug weld size of 0.38”. But, as you can see, this is a big lug, and in some cases it would be hard to find room to weld two of these lugs to the shell without interfering with nozzles, ladder or platform clips, etc.

A second and much better method would be to weld a doubler pad to the shell with a four sided weld and weld the lug plate to it with a three sided weld as shown in the top head drawing above. Therefore a third run of the plate lug program is required. Note from the second run that the four sided weld size is 0.41”, so we need to size a doubler pad such that the four sided weld size required is 0.38” or less. In the second run above, change the width of the lug base to 30.0” and the side weld length to 18.0”. These will be the dimensions of the doubler pad and not the lug plate. Calculate and note that the four-sided weld size required is now 0.33”. Therefore, a 0.75” thick x 18” high x 30” wide double pad could be welded to the shell with a 0.38” four sided weld and the lug plate could be welded to it with a 0.75” three sided weld as shown on the top head drawing. Save this as a third run for your documentation. Mark out all other output information from this run as the only value that is of interest is the value of the four sided weld.

To recap, the bearing and the end area of the lug were calculated from the first run where the maximum force of 170 kips occurred when the vessel was in the vertical. The maximum combined stress for the lug plate and the weld were calculated from the second run where the force on the lug of 68 kips occurred when the vessel was at a lift angle of 0 degrees. The four-sided weld size required to weld a doubler pad to the shell was calculated from the third run where the force on the lug of 68 kips occurred when the vessel was at a lift angle of 0 degrees, the width of the double pad was 30” and the side weld was 18”.

EXAMPLE 3:

Lowering the eccentricity can reduce the combined stress of the lug plate and the lug weld size. Cutting off the bottom segment of the lug pads can accomplish this. To see how this can be done, go to example 3 in the HELP file for the pad eye lugs. This example applies to plate lugs as well as pad eye lugs.

END OF HELP FILE